بسم الله الرحمن الرحيم
في درس سابق تعرفنا على طريقة دراسة إشارة ثلاثية الحدود من الدرجة الثانية على مجموعة الأعداد الحقيقية IR، سنستغل هذه الطريقة لحل متراجحات من الدرجة الثانية بمجهول واحد.
حل في مجموعة الأعداد الحقيقية متراجحة من الدرجة الثانية بمجهول واحد،
يعني تحديد مجموعة القيم العددية التي يحقق فيها المجهول المتفاوتة
المعطاة. فيما يلي مجموعة من الأمثلة المحلولة تشرح طريقة حل هذا النوع من
المتراجحات بإستعمال المميز و جدول الإشارة :
تعريف :
تعريف : نعتبر ثلاثية الحدود : P(x) = ax² + bx + c
كل متفاوتة على الشكل : P(x) < 0 أو P(x) > 0 أو P(x) ≥ 0 أو P(x) ≤ 0 تسمى متراجحة من الدرجة الثانية.
كل متفاوتة على الشكل : P(x) < 0 أو P(x) > 0 أو P(x) ≥ 0 أو P(x) ≤ 0 تسمى متراجحة من الدرجة الثانية.
بصفة عامة :
 |
| دراسة إشارة ثلاثية الحدود : ax² + bx + c |
أمثلة تطبيقية :
حل في IR المتراجحات التالية :
(1) : لنحل في IR المتراجحة : 3x² - 2x - 8 > 0
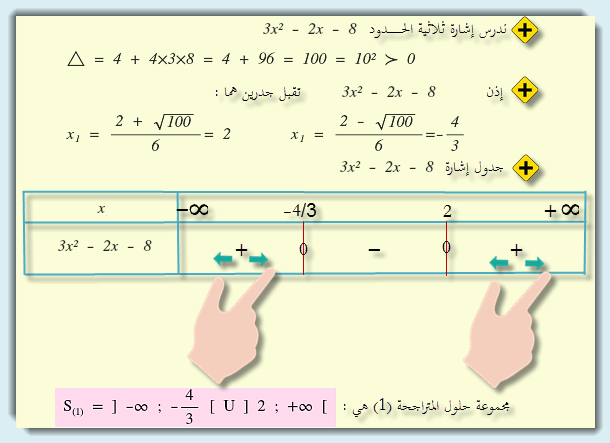
(2) : لنحل في IR المتراجحة : x² - 2x + 15 ≤ 0
(3) : لنحل في IR المتراجحة (3) :
